When considering the linear inequality x – 2y ≥ –12, it’s important to determine which graph accurately represents this equation. By analyzing the inequality and its components, we can identify the correct graph that satisfies the given conditions.
To begin, let’s break down the inequality: x – 2y ≥ –12. This means that any point (x, y) on the graph must satisfy the condition where x minus twice y is greater than or equal to negative twelve. In other words, all points above or on the line should fulfill this criteria.
To find the specific graph for this linear inequality, we’ll need to first transform it into slope-intercept form (y = mx + b), where m represents the slope and b denotes the y-intercept. By rearranging our inequality equation in this form, we can easily visualize how it will be represented on a graph.
Which Is The Graph Of Linear Inequality X – 2y ≥ –12?
Solving the Linear Inequality
To determine the graph of the linear inequality x – 2y ≥ -12, we first need to solve it for y. Let’s begin by isolating y on one side of the equation:
x – 2y ≥ -12 -2y ≥ -x – 12
Next, we divide both sides of the inequality by -2. Remember that when dividing or multiplying an inequality by a negative number, we need to reverse the inequality sign:
(-2y) / (-2) ≤ (-x – 12) / (-2) y ≤ (1/2)x + 6
Now that we have solved for y in terms of x, we can move on to identifying the critical points.

Plotting the Equation on a Graph
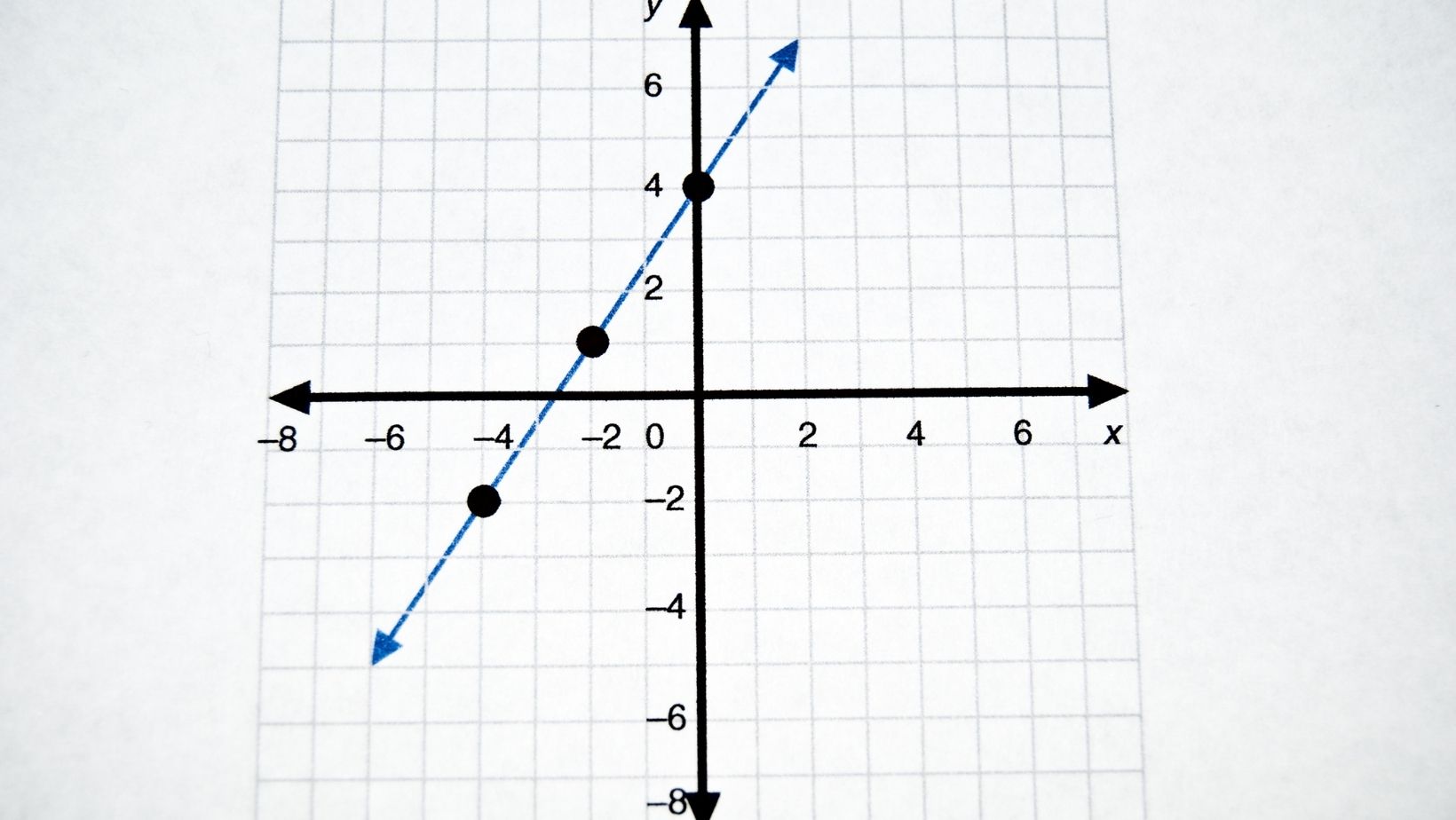
To plot the graph of this linear inequality, we’ll use the slope-intercept form (y = mx + b). The equation for our inequality is y ≤ (1/2)x + 6, where m represents the slope and b represents the y-intercept.
Since m = 1/2, we know that for every unit increase in x, y will increase by half a unit. The y-intercept is 6, which means that when x = 0, y will be equal to 6.
Starting from the point (0, 6), we can draw a line with a slope of 1/2. However, since our inequality includes “less than or equal to,” we need to shade below this line to represent all values of y that are less than or equal to (1/2)x + 6.
By shading below the line and including any points on it, we have successfully represented the graph of the linear inequality x – 2y ≥ -12.
Remember that graphs of inequalities extend infinitely in both directions unless specified otherwise. Solving for y in terms of x in the linear inequality x – 2y ≥ –12 can help us determine which graph represents the solution. Let’s break it down step by step.
- Start with the given inequality: x – 2y ≥ –12.
- To solve for y, we need to isolate it on one side of the inequality symbol.
- Begin by subtracting x from both sides: -2y ≥ -12 – x.
- Next, divide both sides by -2 (remember to reverse the inequality sign when dividing by a negative number): y ≤ (x + 12)/2.
Now that we have solved for y in terms of x, we can analyze the resulting expression and understand how it relates to the graph.
The expression y ≤ (x + 12)/2 represents a region below or on the line defined by y = (x + 12)/2. This line has a slope of 1/2 and a y-intercept at (0,6).
To visualize this graph, plot points on either side of the line and shade in the area that satisfies the original inequality. In this case, since it is “less than or equal to,” you would shade below or along with the line.
Remember that if there is an equality symbol in your original equation or inequality (‘=’,’≥’, ‘≤’), you should draw a solid line to represent that boundary. If there is only an inequality symbol (‘>’, ‘<‘), use a dashed line instead.
By following these steps and understanding how to solve for y in terms of x, we can confidently identify which graph accurately represents the linear inequality x – 2y ≥ –12.